Dr. Anozie Ebigbo, ETH Zurich
Powei Huang, ETH Zurich
Description
Introduction
 Hierarchy of scales as it pertains to the concept of the proposed hybrid model. Assuming that validity criteria are not fulfilled in part of the macroscale model, the pore-network model is used only in that part and connected to the rest of the macroscale domain. Similarly, reaction rates in pore elements of the pore network in which upscaling conditions are not met are corrected either explicitly or by direct simulation.
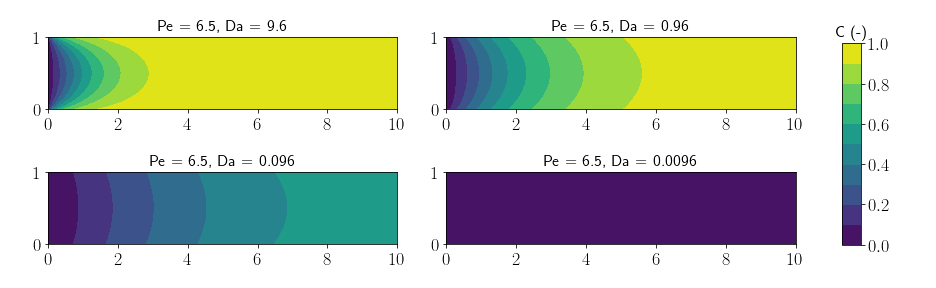
Mineral reaction rates in porous media, i.e. precipitation and dissolution, usually exhibit spatial scaling effects. There is a tendency for apparent reaction rates to decrease as one moves from the pore scale through the laboratory scale to the field scale. Mathematical models at the Darcy scale are often incapable of capturing pore-scale reactive-transport processes (Battiato et al. 2009). Geochemical reaction rates are known to be much lower in the field than when measured in the lab (White and Brantley 2003). Understanding and quantifying these scaling effects is one of the central challenges in the field of subsurface reactive transport.
Hierarchy of scales as it pertains to the concept of the proposed hybrid model. Assuming that validity criteria are not fulfilled in part of the macroscale model, the pore-network model is used only in that part and connected to the rest of the macroscale domain. Similarly, reaction rates in pore elements of the pore network in which upscaling conditions are not met are corrected either explicitly or by direct simulation.
Mineral reaction rates in porous media, i.e. precipitation and dissolution, usually exhibit spatial scaling effects. There is a tendency for apparent reaction rates to decrease as one moves from the pore scale through the laboratory scale to the field scale. Mathematical models at the Darcy scale are often incapable of capturing pore-scale reactive-transport processes (Battiato et al. 2009). Geochemical reaction rates are known to be much lower in the field than when measured in the lab (White and Brantley 2003). Understanding and quantifying these scaling effects is one of the central challenges in the field of subsurface reactive transport.
There are certainly numerous reasons for the discrepancies in reaction rates (Noiriel et al. 2012; Steefel et al. 2015). One important reason lies in the simple fact that upscaled equations do not capture small-scale heterogeneities – in concentration, reactive surface area, flow paths – which are important in capturing the effective reaction rates (Kechagia et al. 2002; Li et al. 2006; Meile and Tuncay 2006; Battiato et al. 2011; Boso and Battiato 2013). In particular, two effects pertaining to mineral precipitation and dissolution are differentiated here:
- When reaction rates are fast compared to the diffusion process, non-negligible concentration gradients can occur within a single pore;
- The heterogeneous nature of subsurface porous media (complicated geometry, uneven distribution of reactive surfaces) can cause nominally reactive parts of the porous medium to be cut off from the main flow paths, leading to lower effective reaction rates at the macroscale (which encompasses a large number of pores) than at the microscale.
Both of these cases, which involve scaling effects between the scale at which reactive transport processes can accurately be described (i.e. the pore scale) and the laboratory scale, will be investigated in this project. The primary aim of the project hence is to elucidate the relevant mechanisms which give rise to such effects. This will be done with numerical modelling.
While numerical models at the pore scale are accurate, they are computationally expensive and often infeasible for the description of laboratory-scale observations, let alone reservoir-scale processes. In order to circumvent this problem without compromising accuracy, a hybrid model, which spatially couples micro- and macroscale models, will be developed. The approach here is to use a microscale model in those parts of the model domain where it is necessary to guarantee accuracy and a macroscale model throughout the rest of the domain. In terms of computational effort, particular attention will be paid to the applicability of the model to laboratory-scale processes, which will be achieved by representing the microscale with pore-network models.
References
- Battiato, I., Tartakovsky, D. M., Tartakovsky, A. M., and Scheibe, T. (2009). ‘On breakdown of macroscopic models of mixing-controlled heterogeneous reactions in porous media’. In: Advances in Water Resources 32, pp. 1664–1673.
- White, A. F. and Brantley, S. L. (2003). ‘The effect of time on the weathering of silicate minerals: why do weathering rates differ in the laboratory and field?’ In: Chemical Geology 202.3–4. Controls on Chemical Weathering, pp. 479–506.
- Noiriel, C., Steefel, C. I., Yang, L., and Ajo-Franklin, J. (2012). ‘Upscaling calcium carbonate precipitation rates from pore to continuum scale’. In: Chemical Geology 318–319, pp. 60–74.
- Steefel, C. I., Beckingham, L. E., and Landrot, G. (2015). ‘Micro-Continuum Approaches for Modeling Pore-Scale Geochemical Processes’. In: Reviews in Mineralogy and Geochemistry 80.1, pp. 217–246.
- Kechagia, P. E., Tsimpanogiannis, I. N., Yortsos, Y. C., and Lichtner, P. C. (2002). ‘On the upscaling of reaction-transport processes in porous media with fast or finite kinetics’. In: Chemical Engineering Science 57.13, pp. 2565–2577.
- Li, L., Peters, C. A., and Celia, M. A. (2006). ‘Upscaling geochemical reaction rates using pore-scale network modeling’. In: Advances in Water Resources 29.9, pp. 1351–1370.
- Meile, C. and Tuncay, K. (2006). ‘Scale dependence of reaction rates in porous media’. In: Advances in Water Resources 29.1, pp. 62–71.
- Battiato, I., Tartakovsky, D. M., Tartakovsky, A. M., and Scheibe, T. (2011). ‘Hybrid models of reactive transport in porous and fractured media’. In: Advances in Water Resources 34.9. New Computational Methods and Software Tools, pp. 1140–1150.
- Boso, F. and Battiato, I. (2013). ‘Homogenizability conditions for multicomponent reactive transport’. In: Advances in Water Resources 62, Part B. A tribute to Stephen Whitaker, pp. 254–265.