PROJECTS
Prof. Martin O. Saar, ETH Zürich
Dr. Anozie Ebigbo, ETH Zürich
Philipp Schädle, ETH Zürich
Introduction
Introduction
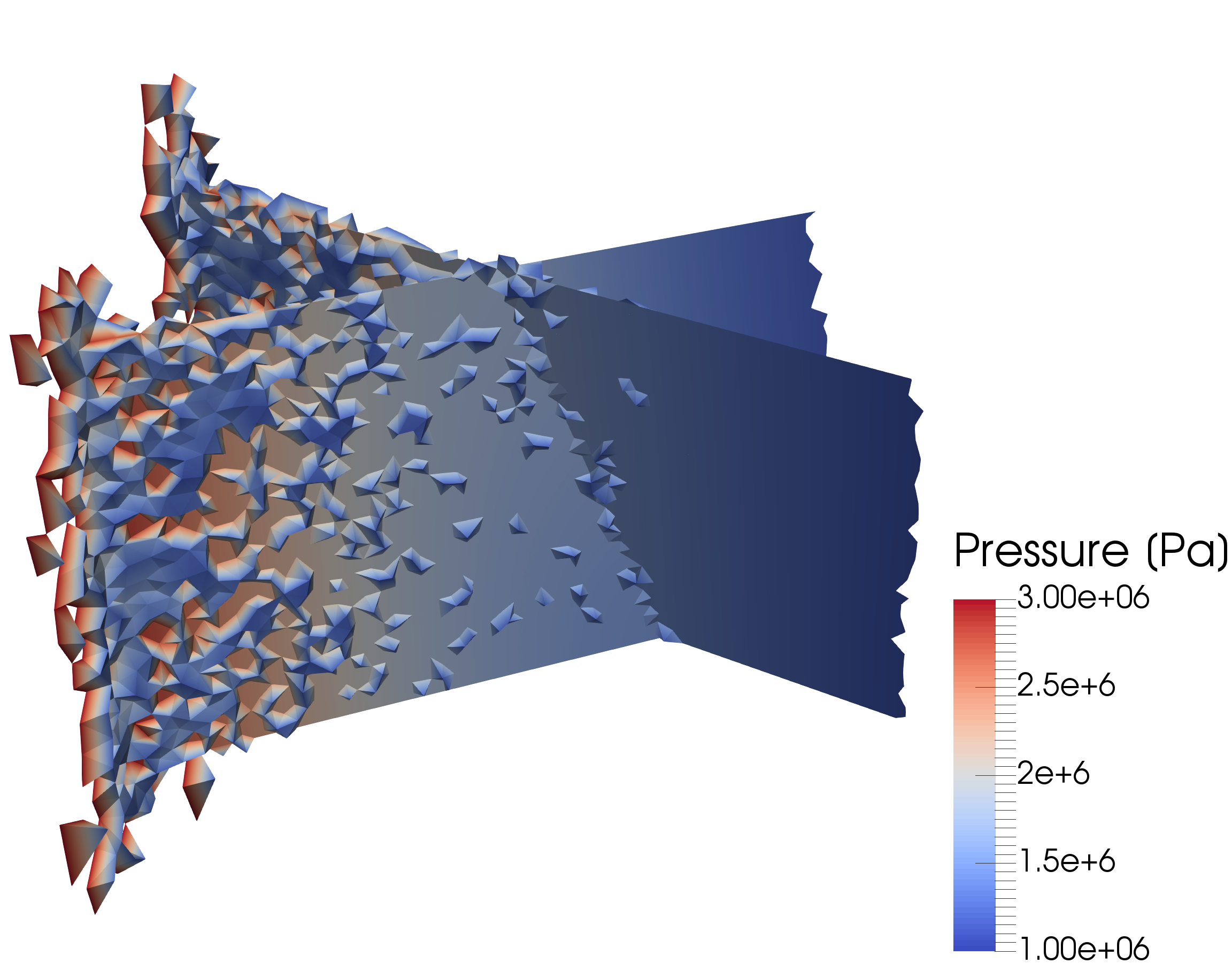
Example of a 2D fracture network, based on the Sotra island near Bergen, Norway [Flemisch, 2017]. The pressure propagates along the pressure gradient from top to bottom. The normalized velocity shows that, in some fractures, the velocity is significantly higher than in others, particularly dead-end fractures are less affected by flow.
Characterizing flow and transport through fracture networks in low permeable rocks is a key question for many energy- and groundwater-related applications [Berkowitz, 2002]. Various computational approaches have been developed to address these problems. One is the discrete fracture network approach (DFN), where the fractures are explicitly represented and form networks. An advantage of using DFNs is that it is possible to account for many different transport phenomena in fractured rock. Flow and transport can be explicitly linked to network characteristics such as fracture (1) density, (2) size, (3) orientation, (4) distribution and (5) aperture.
Fractures of all scales are characterized by two opposite rock surfaces with variable surface roughness and aperture. Due to the variable roughness, the local aperture of these walls is heterogeneous and promotes the formation of channels and barriers within fracture planes. This heterogeneity has a significant effect on flow and transport within fractures. Furthermore, flow and transport depends on the flow direction within a fracture. Thus, the location of the fracture in a network and the connectivity with other fractures are key parameters for the representation of flow and transport. Fluid enters and exits a fracture primarily at intersections with other fractures. Additionally, due to channeling at the network scale, some fractures might be hydraulically disconnected and not affected by flow and transport. Consequently, a combined consideration of fracture-scale heterogeneity and network-scale topology is crucial for flow and transport modeling in fractured reservoirs [de Dreuzy, 2012; Makedonska, 2016].
The large variability in flow velocities mean that the dominant transport processes can differ significantly within a fractured rock mass. In hydraulically connected fractures and, more specifically, in the highly transmissible parts of these fractures, transport is dominated by advection and dispersion. Solute transport due to diffusion becomes more relevant in hydraulically disconnected fractures and in the low transmissible parts of the fractures. Transfer between fractures and rock matrix as well as transport in the rock matrix is dominated by diffusion.
For many applications (e.g. Enhanced Geothermal Systems) heat transport is a key question. While convective heat transport dominates in fractures, the transfer of heat in the rock matrix towards the working fluid is dominated by conduction.
Approach
In this project, we perform numerical simulations in order to increase our understanding of the above-mentioned processes. Furthermore, we aim to find simplifications for the applied methods so that the modeling performance improves. Generic discrete fracture networks are generated based on above-mentioned network characteristics. Various stochastic models apply to the different network parameters. As discussed above, it is crucial to consider a heterogeneous fracture aperture distribution. While the mean fracture aperture is correlated to the fracture size, the aperture at each computational node has a unique value following a stochastic distribution.
Numerical simulations of flow and transport in such heterogeneous model domains are computationally demanding, particularly if multiple realizations need to be performed. To optimize that we only consider large fractures explicitly because they dominate flow and transport. Small fractures are accounted for using effective permeability models. This requires the use of existing upscaling models available in literature [Ebigbo, 2016; Mourzenko, 2011; Saevik, 2013] as well as their application in a robust way to arbitrarily shaped model domains. Furthermore, the effective permeability model needs to be valid for any possible flow direction.
The transmissivity of the fractures is linked to the aperture using the cubic law [Zimmerman, 1994]. Here, we consider a unique value for aperture at each computational node in the model domain. This is in contrast to the widely assumed parallel plate model with a homogeneous aperture for the entire fracture. Solute transport in the model domain is simulated by applying the advection-dispersion diffusion equation. Non-reactive solutes which are not adsorbed at the rock matrix are considered.
This methods are used to study the impact of network-scale and fracture-scale heterogeneities on flow and transport in fractured reservoirs.
Research Goals
In this project we aim for the following research goals:
- Increase knowledge on flow and transport in fractured reservoirs.
- Study the influence of fracture-scale and network-scale heterogeneity on transport.
- Find accurate simplifications to represent discrete fracture networks at the reservoir scale and
- Find robust methods to upscale networks of small fractures in arbitrarily shaped domains.
References
Berkowitz, B. (2002). Characterizing flow and transport in fractured geological media: A review. Advances in Water Resources , 25(8):861-884.
de Dreuzy, J.-R., Meheust, Y., and Pichot, G. (2012). Influence of fracture scale heterogeneity on the flow properties of three-dimensional discrete fracture networks (DFN). Journal of Geophysical Research: Solid Earth, 117(B11):1-21.
Ebigbo, A., Lang, P. S., Paluszny, A., and Zimmerman, R. W. (2016). Inclusion-Based Evective Medium Models for the Permeability of a 3D Fractured Rock Mass. Transport in Porous Media , 113(1):137-158.
Flemisch, B., Berre, I., Boon, W., Fumagalli, A., Schwenck, N., Scotti, A., Stefansson, I., and Tatomir, A. (2017). Benchmarks for single-phase flow in fractured porous media.
Makedonska, N., Hyman, J. D., Karra, S., Painter, S. L., Gable, C. W., and Viswanathan, H. S. (2016). Evaluating the effect of internal aperture variability on transport in kilometer scale discrete fracture networks. Advances in Water Resources , 94(4):486-497.
Mourzenko, V. V., Thovert, J.-F., and Adler, P. M. (2011). Permeability of isotropic and anisotropic fracture networks, from the percolation threshold to very large densities. Physical Review E, 84(3):036307.
Saevik, P. N., Berre, I., Jakobsen, M., and Lien, M. (2013). A 3D Computational Study of Effective Medium Methods Applied to Fractured Media. Transport in Porous Media , 100(1):115-142.
Zimmerman, R. W., Bodvarsson, G. S., and Bodvarsson, G. S. (1994). Hydraulic Conductivity of Rock Fractures. Technical report, Lawrence Berkeley Laboratory University of California, Berkeley, CA 94720.